A new mathematical language for biological networks
New mathematical model of genetic interaction identifies master regulators in biological networks
A team of researchers around Berlin mathematics professor Michael Joswig is presenting a novel concept for the mathematical modeling of genetic interactions in biological systems. Collaborating with biologists from ETH Zurich and Carnegy Science (USA), the team has successfully identified master regulators within the context of an entire genetic network. The research results provide a coherent theoretical framework for analyzing biological networks and have been published in the "Proceedings of the National Academy of Sciences" (PNAS).
Joint press release with the Berlin Cluster of Excellence MATH+
It is a longstanding goal of biologists to determine the key genes and species that have a decisive impact on evolution, ecology, and health. Researchers have now succeeded in identifying certain genes as master regulators in biological networks. These key regulators exert a greater control within the system and steer essential cellular processes. Previous studies have mainly focused on pairwise interactions within the system, which can be strongly affected by genetic background or biological context. "Context-dependent effects are widespread in biology but have not been sufficiently investigated. A major challenge with biological networks is that they are high dimensional. Therefore, for the first time, our team is pursuing a more far-reaching approach that includes higher-order interactions and thus identifies key regulators in the context of the entire network," explains Michael Joswig, who is a Professor for Discrete Mathematics and Geometry at the Technische Universität Berlin, a Distinguished Fellow of the Berlin Cluster of Excellence MATH+, as well as a group leader at the Max Planck Institute for Mathematics in the Sciences in Leipzig.
The concept of epistasis as an approach for high-dimensional geometric modeling
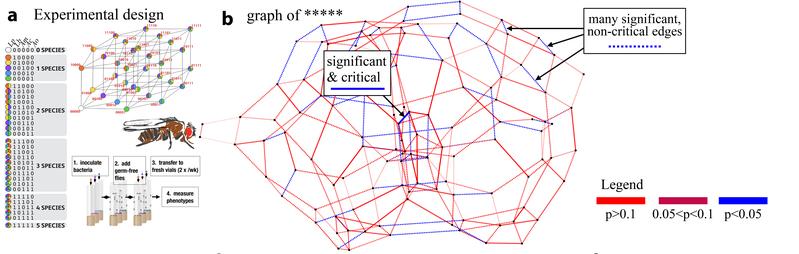
The scientists examined real data sets provided by biologists who analyzed the life expectancy of the fruit fly Drosophila based on the presence of certain combinations of bacteria in the gut. In order to describe these processes mathematically, the team applied a high-dimensional approach from geometry, reinterpreting the well-known biological concept of epistasis. Epistasis refers to an interaction phenomenon between different genes, wherein one gene may influence the appearance of another. These interactions are crucial for understanding genetic inheritance and the diversity of phenotypes, revealing how different genes interact to regulate the expression of specific traits. Epistatic interactions hold great significance in nature; for instance, epistasis between bacteria in the microbiome can have far-reaching functional consequences.
The researchers analyzed the microbiome of an entire population of fruit flies with five different bacterial species, alongside measurements of the flies’ life expectancy under certain combinations of these bacteria, representing the phenotype. Relevant biological information was mapped using adaptive landscapes, known as fitness landscapes, and their epistasis quantified in order to investigate how individual genes and species influence interactions in the entire biological network. The resulting 5-dimensional data sets were analyzed again and graphically presented.
Identification of relevant signals as master regulators of the network
The primary contribution of this work, which not only presents the researchers' previous findings in a new language but also reinterprets the previous work by Niko Beerenwinkel, Lior Prachter, and Bernd Sturmfels, lies in representing fitness landscapes as epistatic filtration of the network. This method enables the analysis of concrete experiments to encode relevant biological information, making it readable (interpretable) and allowing the identification of relevant signals in higher dimensions that serve as master regulators of the network.
This interdisciplinary study at the intersection of biology and mathematics involves numerous real experiments to demonstrate the capability of the proposed method in detecting biologically relevant information and its reliable signals while avoiding false positives. The outcome provides a coherent theoretical framework for analyzing biological networks.
Coherent theoretical framework for analyzing whole networks
In the fruit fly experiment described above, the entire genetic interaction involves five different gene types or bacteria, with each genotype comprising a combination of 32 genes. This data set serves as the foundation for drawing conclusions about the life expectancy of the fly. An important consideration is, what happens when additional genes or parameters occur–a common real-life scenario. Due to its coherent geometric superstructure, the new method provides a flexible framework for detecting and describing deviating scenarios, something unattainable in previous experiments and mathematical modeling, which required a separate evaluation for each individual experiment.
"We are excited to contribute to describing biological results in a mathematical language. Through our geometric-statistical analysis method, we hope to provide a powerful tool for exploring biological networks in higher dimensions. It has proven to be an excellent way of identifying the master regulators of networks. By applying the new high-dimensional geometric approach, which quantifies epistasis in a fitness landscape, we were able to decipher how individual genes and species influence interactions in the broader biological network," concludes Michael Joswig.
The microbiotic composition in the gut significantly influences life expectancy, and it would be desirable to apply this new quantification method to humans as well. However, due to the vast number of bacteria in the human gut, this is not yet possible. The scientists hope that future developments using simpler methods, in combination with classic transformation processes, could pave the way for applications such as the development of customized drugs.
Wissenschaftlicher Ansprechpartner:
Prof. Dr. Michael Joswig joswig@math.tu-berlin.de
https://page.math.tu-berlin.de/~joswig/
Originalpublikation:
Holger Eble, Michael Joswig, Lisa Lamberti und William B. Ludington
Master regulators of biological systems in higher dimensions
In Proceedings of the National Academy of Sciences” (PNAS)
DOI: https://doi.org/10.1073/pnas.2300634120
Ähnliche Pressemitteilungen im idw