Ein neuer mathematischer Ansatz zum Verständnis der Dynamik natürlicher Systeme
Ein Forscherteam hat einen neuen mathematischen Ansatz entwickelt, der es erstmals ermöglicht, das lang anhaltende vorübergehende Verhalten in komplexen Systemen zu beschreiben. Sie führen "ghost channels" und "ghost cycles" als neuartige Konzepte ein, die erklären, wie natürliche Systeme über längere Zeiträume stabil bleiben können und dennoch schnell in einen anderen Zustand übergehen können. Dies könnte uns helfen, Kipp-Kaskaden zu verstehen, die beispielsweise die biologische Vielfalt oder die Folgen der Eisschmelze in der Arktis beeinflussen, sowie die neuronale Dynamik, die beispielsweise bestimmt, wie wir Geschmack kodieren.
Wissenschaftler und Wissenschaftlerinnen weltweit nutzen Modellierungsansätze, um komplexe natürliche Systeme wie Klimasysteme, neuronale Netzwerke oder biochemische Netzwerke zu verstehen. Ein Forscherteam hat nun einen neuen mathematischen Ansatz entwickelt, der erstmals einen Mechanismus erklärt, der lang anhaltendes vorübergehendes Verhalten in komplexen Systemen ermöglicht. Sie führen "ghost channels" und "ghost cycles" als neuartige Konzepte ein, die aufzeigen, wie natürliche Systeme über längere Zeiträume stabil bleiben und dennoch schnell in einen anderen Zustand übergehen können. Dieser neue Ansatz stellt das traditionelle Konzept stabiler oder instabiler Gleichgewichte in Frage und könnte uns helfen, besser zu verstehen, wie vorübergehend stabile neuronale Dynamiken die sensorische Informationsverarbeitung steuern oder wie man Kipp-Kaskaden vorhersagen kann, die beispielsweise zum Verlust der Artenvielfalt führen. Die gemeinsame Studie des Max-Planck-Instituts für Neurobiologie des Verhaltens - caesar, der University of Leicester und des King's College London wurde in der renommierten Zeitschrift Physical Review Letters veröffentlicht.
Fragen wir in einer fremden Stadt nach dem Weg, so speichert unser Arbeitsgedächtnis vorübergehend Informationen wie Abzweigungen oder Sehenswürdigkeiten, denen wir in einer bestimmten Reihenfolge folgen müssen. Sobald das Ziel erreicht ist, werden diese Details jedoch wieder vergessen. Um diese Aufgabe zu bewältigen, können die neuronalen Netzwerke in unserem Gehirn die neuronale Aktivität vorübergehend stabilisieren. So können wir uns an die notwendigen Informationen erinnern und dennoch schnell in ein anderes Stadium innerhalb der Sequenz wechseln.
Eine ähnliche Dynamik kann auch in der Ökologie beobachtet werden. In konkurrierenden Mikrobenpopulationen kann oft eine Art über lange Zeit dominieren und ein stabiles Gleichgewicht schaffen. Plötzlich, und ohne ersichtlichen Grund, beginnt jedoch eine andere Art, die Oberhand zu gewinnen, was zu einem Rückgang der zuvor dominierenden Art führt. Solche Übergänge können sogar zum Aussterben von Arten und zum Verlust der biologischen Vielfalt führen. Um vorherzusagen, ob und wann ein solches Kipp-Phänomen eintreten könnte, wird häufig die Dynamik vor der Veränderung analysiert. Die Herausforderung bei solchen Vorhersagen liegt darin, dass sie Vorwissen darüber erfordern, ob es sich tatsächlich um einen stabilen Zustand oder eine lange Übergangsphase handelt, um die aufgezeichneten Daten korrekt zu interpretieren. Bei wirtschaftlich wichtigen Ökosystemen wie Korallenriffen ist es daher entscheidend, festzustellen, ob Riffe, die zunächst gesund erscheinen, tatsächlich Gefahr laufen, in einen von Algen dominierten Zustand zu kippen.
Traditionelle Dynamikmodelle auf dem Prüfstand
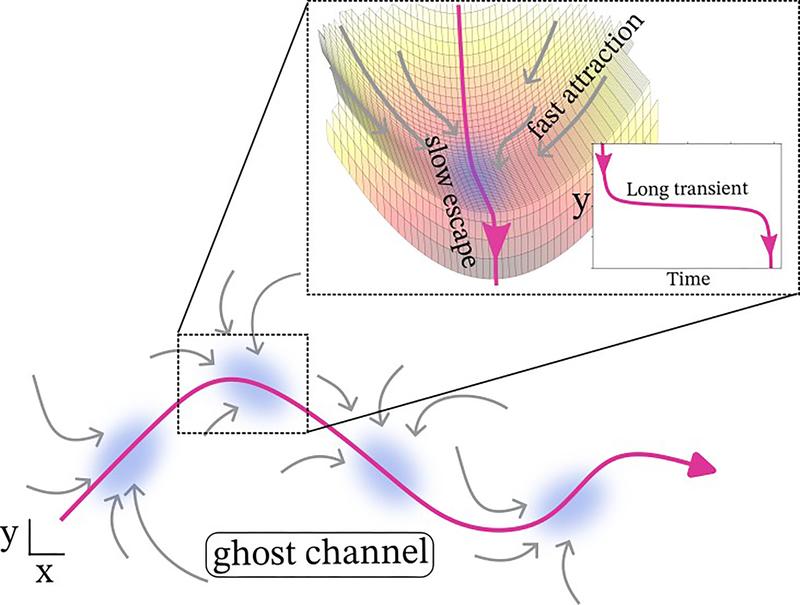
Klassischerweise werden die dynamischen Zustände komplexer Systeme als Attraktoren oder Gleichgewichte beschrieben—abstrakte mathematische Konzepte, von denen erwartet wird, dass sie über einen unendlich langen Zeitraum stabil bleiben und zu denen das System nach kleinen Störungen zurückkehrt. Diese Zustände erfassen jedoch nicht, wie vorübergehende Stabilität und schnelle Übergänge erreicht werden können. Um beide Eigenschaften zu berücksichtigen, wurden bisher Sequenzen dynamischer „Sattel“-punkte untersucht. Ähnlich wie ein Sattel stabilisiert diese Struktur die Dynamik entlang einer Dimension—dem Sitz des Sattels—ist jedoch von Natur aus instabil und kann entlang der orthogonalen Dimension abfallen. Wenn die instabile Dimension eines Sattels mit der stabilen Dimension eines anderen Sattels verbunden wird, kann ein Kanal von Sätteln, ein sogenannter „heterokliner Kanal“, entstehen. Auf diese Weise kann die Dynamik des Systems in einer Folge von Zuständen wechseln.
In einer Studie unter der Leitung von Forschenden des Max-Planck-Instituts für Neurobiologie des Verhaltens in Bonn (MPINB), in Zusammenarbeit mit der University of Leicester und dem King’s College London, wurde gezeigt, dass heterocline Kanäle die in realen, verrauschten Systemen beobachtete Dynamik nicht vollständig erfassen können. Die Fähigkeit, vorübergehend stabile Zustände entlang des Sattels zu erzeugen, geht verloren, sobald das System auch nur kleine Störungen erfährt. Im Gegensatz dazu haben die Forscher spezielle Instabilitätsarten identifiziert—sogenannte „ghost channels“ und „ghost cycles“—die erklären, wie komplexe Systeme robustes, vorübergehend stabiles Verhalten zeigen können, bevor sie schnell in einen anderen vorübergehend stabilen Zustand übergehen, der völlig unterschiedliche Eigenschaften aufweisen kann. Diese „Geisterstrukturen“ treten auf, wenn ein System an der Grenze zwischen zwei oder mehr qualitativ unterschiedlichen Regimen balanciert. Diese Organisation ermöglicht es Systemen, verschiedene Regime zu nutzen und effektiv zwischen gegensätzlichen Eigenschaften auszugleichen.
Dr. Akhilesh Nandan vom MPINB erläutert: „Indem wir den Rahmen, der die Dynamik stabiler Zustände oder Attraktoren beschreibt, durch einen neuen Rahmen ersetzt haben, in dem die Dynamik formal instabiler Strukturen, wie etwa ghost channels, bestimmt wird, konnten wir eine mögliche Erklärung für das liefern, was experimentell in einer Vielzahl von Systemen beobachtet wurde. Entscheidender Bestandteil dieses neuen Rahmens war die mathematische Charakterisierung dieser abstrakten Strukturen.“
Verstehen von degradierten Ökosystemen und Klimawandel
In ihrer Veröffentlichung zeigen die Wissenschaftler*innen, dass ghost-basierte Gerüste die Eigenschaften langer Transienten in verrauschten Systemen besser erfassen als herkömmliche Modelle. Anstatt sich auf die Charakterisierung von (un)stabilen Fixpunkten zu stützen, konzentriert sich dieses neuartige Modell auf langsame Trajektorien, die durch ghosts in Kanälen und Zyklen organisiert werden.
Eine bedeutende Schlussfolgerung aus dieser Studie ist, dass diese ghost-Strukturen eine Vielzahl von Prozessen in biologischen und natürlichen Systemen beleuchten können, wenn man weiß, worauf man achten muss. „Wir haben ghost-basierte Strukturen in Modellen identifiziert, die im Kontext zellulärer Entscheidungsprozesse während der Entwicklung relevant sind, aber auch in Modellen von Kippkaskaden in Klimasystemen, die untersucht werden, um zu erforschen, wie ein Kippen, beispielsweise der atlantischen meridionalen Umwälzzirkulation (Atlantic Meridional Overturning Circulation, AMOC), die Dynamik anderer Klima-Subsysteme beeinflussen könnte“, erklärt Dr. Daniel Koch. Diese neuen Erkenntnisse eröffnen viele Perspektiven für die zukünftige Forschung, von einem besseren theoretischen Verständnis der Kodierung von Geruch oder Geschmack in neuronalen Netzwerken bis hin zu genaueren Vorhersagen von Veränderungen in Ökosystemen oder dem Klima.
„Was uns besonders begeistert, ist das Potenzial dieses leistungsstarken theoretischen Rahmens für die biologische und künstliche Intelligenzforschung“, sagt Dr. Aneta Koseska, die am MPINB in Bonn die Gruppe für „Zelluläre Komputationen und Lernen“ leitet. „Wir haben bereits begonnen zu untersuchen, wie Geisterstrukturen das Lernen in natürlichen und künstlichen neuronalen Netzwerken unterstützen können, und wie sie dazu beitragen können, die derzeitigen Herausforderungen des katastrophalen Vergessens zu überwinden.“
Dieses Modell könnte daher ein vielversprechendes Fundament für die Untersuchung langer Transienten bieten und gleichzeitig die Grenzen bestehender mathematischer Ansätze aufzeigen, sowie verdeutlichen, wo weitere Erweiterungen erforderlich sind, um langjährige offene Fragen zur quasistabilen transienten Dynamik in lebenden, natürlichen und künstlichen Systemen zu adressieren.
Wissenschaftlicher Ansprechpartner:
Dr. Aneta Koseska, aneta.koseska@mpinb.mpg.de
Originalpublikation:
https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.133.047202
Weitere Informationen:
https://mpinb.mpg.de/de/presse-outreach/pressemitteilungen/2024/duplikat-von-new-mathematical-framework-to-understand-dynamics-of-natural-systems.html
Ähnliche Pressemitteilungen im idw